Given a natural number $n$, the Euler $\varphi$ function, also known as Euler’s Totient, applied to $n$ represents the number of positive numbers less than $n$ that are coprime with $n$.

Prime Power

Proposition. For a prime number $p$ and a natural number $n$:

$$ \varphi(p^n) = p^n (1 - \frac{1}{p}) $$

Proof

Create a list of the numbers less than $p^n$ and count how many numbers in the list are not relatively prime to $p^n$.

Because $p$ is prime we are counting the multiples of $p$ that are less than $p^n$. There are $p^{n-1}$ such multiples, they are:

$$ \set{ 0, p, 2p, \ldots, p^{n-1} p } $$

Thus, among the first $p^n$ numbers, $p^n - p^{n-1} = p^n (1 - 1/p)$ are coprime with $p^n$ ∎

Corollary. If $p$ is prime then $\varphi(p) = p - 1$.

Proof. Trivially follows the previous proposition for $n = 1$ ∎

Product of Primes

Proposition. For two primes $p$ and $q$,

$$ \varphi(pq) = \varphi(p) \varphi(q). $$

Proof

Given two primes $p$ and $q$, the elements $x < pq$ such that $\gcd(x, pq) \neq 1$ are:

• $A = \set{ 0 }$
• $B = \set { p, 2p, 3p, \dots, (q-1)p }$
• $C = \set { q, 2q, 3q, \dots, (p-1)q }$

The three sets are disjoint.

That is, if $ip = jq \implies q \mid (ip) \implies q \mid i$, and this is impossible because $i < q$.

Follows that:

$$ \varphi(pq) = |\mathbb{Z}_{pq}| - (|A| + |B| + |C|) = pq - (1 + (p-1) + (q-1)) = (p-1)(q-1) = \varphi(p)\varphi(q) $$

∎

Product of Coprimes

Proposition. If $m$ and $n$ are coprime then $\varphi(mn) = \varphi(m)·\varphi(n)$

Proof Construct the table of numbers from $0$ to $mn - 1$ with $m$ rows and $n$ columns.

	0	1	2	…	j	…	(n-1)
$0$	$m+0$	$m+1$	$2m+0$	…	$jm+0$	…	$(n-1)m+0$
$1$	$m+1$	$2m+1$	$2m+1$	…	$jm+1$	…	$(n-1)m+1$
…	…	…	…	…	…	…	…
$i$	$m+i$	$m+i$	$2m+i$	…	$jm+i$	…	$(n-1)m+i$
…	…	…	…	…	…	…	…
$m-1$	$m+(m-1)$	$m+(m-1)$	$2m+(m-1)$	…	$jm+(m-1)$	…	$(n-1)m+(m-1)$

Proof (Alt). See CRT applications.

General Formula

The generic closed form formula for the sequence is:

φ(n) = n · ∏ (1 - 1/pᵢ)

With {pᵢ} the primes in the factorization of n.

Proof

From the above propositions and the fundamental theorem of arithmetic:

φ(n) = φ(∏ pᵢ^eᵢ) = ∏ φ(pᵢ^eᵢ) = ∏ pᵢ^eᵢ·(1 - 1/pᵢ) = n·∏(1 - 1/pᵢ)

Some values for the function

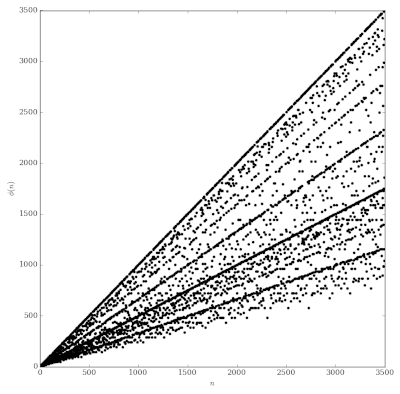
As can be easily seen from the table and the graph, the function is not monotonic.

n	φ(n)
1	1
2	1
3	2
4	2
5	4
6	2
7	6
8	4
9	6
10	4
11	10
12	4
13	12
14	6
15	8
16	8
17	16
18	6
19	18
20	8
21	12
22	10
23	22
24	8
25	20
26	12
27	18
28	12
29	28
30	8
31	30
32	16
33	20
34	16
35	24
36	12
37	36
38	18
39	24
40	16
41	40
42	12
43	42
44	20
45	24
46	22
47	46
48	16
49	42
50	20
51	32
52	24
53	52
54	18
55	40
56	24
57	36
58	28
59	58
60	16
61	60
62	30
63	36
64	32
65	48
66	20
67	66
68	32
69	44

References

• Modular Arithmetic Basics
• Chinese Remainder Theorem
• Sequence A000010 in the OEIS
• Wikipedia