Data-Origin Authentication: the process of verifying that the data comes from the source it claims coming from. This is typically done using some cryptographic technique such as digital signatures or message authentication codes.

Peer-Entity Authentication: the process of verifying the identity of a communicating actor, such as a user or a device. This is typically done using methods such as passwords, biometric authentication or digital certificates.

In other words data-origin authentication is about verifying the source of the data, while peer-entity authentication is more about verifying the identity of the sender (or recipient) the data.

A security service which often comes bounded with authentication is data integrity, which allows the recipient to detect if a message has been tampered during transmission.

Note that modifications to messages are not always introduced by a malicious actor, alterations may be due to networking or physical issues.

Simple Protocols

Using One-Way Functions

Alice wants to authenticate to Bob’s using a secret password or passphrase. Bob holds the one-way hash function output of Alice’s secret.

1. Alice sends to Bob her password.
2. Bob performs a one-way hash function on the password.
3. Bob compares the result with the value it previously stored.

Bob doesn’t store the table of everybody’s valid password in cleartext, thus the threat of someone breaking into the host and steal the passwords is a bit mitigated.

Dictionary attack

Mallory can compile offline a list of very common passwords and apply the one-way function to the list. Mallory then compares the results to each of the hashed passwords list. If a match is found then Mallory found the secret.

Salt

A random string concatenated with the password before being fed to a one-way function.

Typically, a different salt is used for each different secret. Both the salt and the result of the one-way function are stored in the Bob’s host.

Salt mitigates dictionary attack. Mallory has to do a trial of each password in his dictionary every time he tries to break a different person’s password, rather that just doing one massive pre-computation for all possible passwords and have it ready for other host to attack.

Eavesdropping

If the password is sent in clear-text then Eve, can trivially intercept it. It is thus recommended to enforce the scheme with a cryptographic protocol which provides confidentiality.

However, if Eve has access to the authentication host, then it can read it from a memory dump, before the host hash it for further checks.

S/KEY One-Time Passwords

At system initialization time:

1. Alice enters a random number, r.
2. The authentication host computes { x₁ = f(r), .. , xₙ = f(xₙ₋₁) }. Alice puts this list away.
3. The authentication host stores xₙ₊₁ in a database next to Alice’s name.

To log-in:

1. Alice enters xₙ
2. The host computes f(xₙ) and check if matches the value xₙ₊₁ saved in the database.
3. If matches, Alice is authenticated and the value xₙ₊₁ is replaced with xₙ in the database.

If the host database stores the value xᵢ then Alice authenticates with the value xᵢ₋₁.

When Alice runs out of numbers the system should be reinitialized.

With the expiration of the basic patents on public-key cryptography and the widespread usage of SSH and other strong cryptographic protocols that can secure an entire session, not just the password, S/KEY is falling in disuse.

Shared Key Authentication

We assume an encryption algorithm with some form of avalanche effect.

c = E(k, m)

If the encrypted message c is altered, then almost surely we end up decrypting some junk.

Assuming that we are able to distinguish junk from a legit message then the encryption function gives us some kind of integrity check service.

If our end-goal is to only provide integrity and authentication, and we don’t require for the function to be reversible, there are more efficient ways to provide the same service.

Message Authentication Codes

A MAC is a cryptographic hash function which output also depends on a secret k.

h = H(k, m)  

The MAC h is typically shared together with the message.

Everyone that has the secret key k can check m' by computing H(k, m) and comparing the result with the h found together with m'.

One trivial, but not secure, form of MAC is to just hash the concatenation of the message with the key:

h = H(m || k)

Popular secure MAC schemes are HMAC and CMAC.

Mutual authentication protocol

Secret-Key IDentification protocol (SKID) allows two parties to authenticate with each other.

SKID2 allows Alice to prove his identity to Bob and is resistant to replay attacks.

1. Bob chooses a random number b and sends it to Alice.
2. Alice chooses a random number a and sends to Bob a and H(k,a||b||A).
3. Bob computes H(k,a||b||A) and compares it to Alice’s MAC.

SKID3 additionally allows Bob to prove his identity to Alice (mutual authentication).

4. Bob sends to Alice H(k,a||b||B).
5. Alice computes H(k,a||b|||B) and compares it to the Bob’s MAC.

Authentication and Confidentiality

Let’s assume we have two keys, one to encrypt k₁ and one for the MAC k₂.

Encrypt-and-MAC

1. Encrypt the plaintext using k₁;

2. Compute the MAC of the plaintext using k₂;

3. Append the MAC to the ciphertext.

   E(k₁, m) || H(k₂, m)

Provides integrity of the plaintext only.

If the cipher is malleable, the contents of the ciphertext could be altered, but after decryption, we should find an invalid plaintext.

May reveal information about the plaintext in the MAC. This occurs if the plaintext messages are repeated, and the MACed data does not include a nonce.

MAC-then-Encrypt

1. Compute the MAC of the plaintext using k₂;

2. Append the MAC to the plaintext;

3. Encrypt everything using k₁.

   E(k₁, m || H(k₂, m))

Provides integrity of the plaintext only.

If the cipher is malleable it may be possible to alter the message to appear valid and have a valid MAC. This is a theoretical attack, practically speaking a good MAC algorithm and secret should provide good protection.

The MAC doesn’t leak any information on the plaintext, since it is encrypted.

Encrypt-then-MAC

1. Encrypt the plaintext using k₁;

2. Compute the MAC of the ciphertext using k₂;

3. Append the MAC to the ciphertext.

   c = E(k₁, m) c || H(k₂, c)

Provides integrity of both ciphertext and plaintext. We should be able to deduce whether a given ciphertext is indeed authentic or has been forged.

If the cipher scheme is malleable we need not be so concerned since the MAC will filter out any invalid ciphertext.

The MAC does not provide any information on the plaintext since, assuming the output of the cipher appears random, so does the MAC.

In short, Encrypt-then-MAC seems to be the most ideal scheme. Any modifications to the ciphertext that do not also have a valid MAC can be filtered out before decryption, protecting against any attacks on the implementation.

Public Key Authentication

Given the keypair (pub, sec), the owner of the keys can prove message authenticity by digitally signing the message:

s = sign(sec, m)

Everyone can then check if the message is from the owner of pub:

verify(pub, m, s)

Digital signatures also provide non-repudiation property. That is, a valid signature can only be produced by the owner of the keypair and no-one else. This can be proven to any third party.

Typically, what is digitally signed is not m but a hash of the message H(m).

Authentication and Confidentiality

As for MAC, there are three popular approaches:

• Encrypt-And-Sign
• Sign-Then-Encrypt
• Encrypt-then-Sign

The procedures are similar to the ones proposed for MAC and have the same security properties.

Simple Protocols

Bob’s host holds the list of authorized users public keys.

1. Bob sends to Alice a random challenge.
2. Alice signs the challenge with her private key and sends it back.
3. Bob verifies the signature with Alice public key.
4. If the signature is valid then Alice is authenticated.

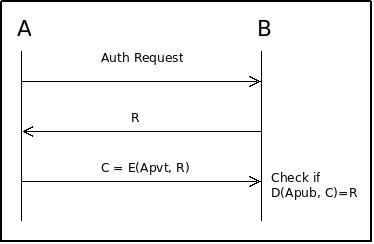
Neither Bob’s host nor the communication channel needs to be secure.

Alice never sends her private key over the transmission network. Eve listening on the interaction can’t get any information that would enable her to impersonate Alice.

A variant is where Bob sends to Alice a challenge encrypted using Alice’s public key. Alice must send back to Bob the decrypted challenge to prove that she is the owner of the private key.

However, for Alice it is not a good practice to encrypt or decrypt arbitrary strings from a potentially rogue authentication hosts.

A more secure protocol takes the following form.

1. Alice encrypts using her private key a random challenge c₁.
2. Bob decrypts the challenge using Alice public key. And gets c₁.
3. Bob sends to Alice a random challenge c₂.
4. Alice applies a public shared function f (e.g. a hash) to c₁||c₂ and sends to Bob the output encrypted using her private key.
5. Bob decrypt the message and checks if the result is equal to the one he computed independently.

With this protocol Alice never encrypts or decrypts strings chosen by Bob and can still prove that she have the correct private key.